Forces motrices dans un système de deux nanoparticules

Considérons un système de deux nanoparticules de tailles différentes. La plus grande nanoparticule est constituée d’un noyau et d’une coquille. L’axe de symétrie du système OZ relie les centres des particules. Supposons que la lumière extérieure tombe sur le système. Pour prouver l’effet de l’interaction entre les particules, nous devons calculer la susceptibilité effective20 pour le système considéré. Il est pratique d’utiliser la fausse méthode de la fonction verte21. Considérons le milieu constitué par l’environnement dans lequel les petites nanoparticules sont incorporées. Soit la sensibilité effective des petites nanoparticules \({\rm X}_{ij}^{(p)}({\mathbf{R}},\omega)\). Notez que la sensibilité effective est une propriété de l’objet et dépend du matériau dont l’objet est fait et des dimensions et de la forme de l’objet. La susceptibilité effective relie la réponse linéaire (polarisation) au champ externe, c’est-à-dire \(P_{i} ({\mathbf{R}},\omega) = \varepsilon_{0}{\rm X}_{ij}^{(p)}({\mathbf{R}},\omega ) E_{j}^{(0)} ({\mathbf{R}},\omega)\)20. Ensuite, le calcul de la sensibilité effective prévoit de prendre en compte les processus d’auto-travail.
La fonction électrodynamique verte de l’environnement est \(G_{ij}^{(0)}({\mathbf{R}},{\mathbf{R}}^{^{\prime}},\omega)\). Ensuite, en utilisant la méthode proposée dans16fonction du pseudo-vide Green \(G_{ij}^{(m)}({\mathbf{R}},{\mathbf{R}}^{^{\prime}},\omega)\) Le « environnement de petites nanoparticules » pour le système peut être écrit comme suit (voir annexe)
$$\start{align} G_{ij}^{(m)}({\mathbf{R}},{\mathbf{R^{\prime}}},\omega) & = G_{ij}^{ (0)} ({\mathbf{R}},{\mathbf{R}}^{^{\prime}},\omega) + G_{ij}^{(R)} ({\mathbf{R} }, {\mathbf{R}}^{^{\prime}},\omega) \\ & = G_{ij}^{(0)}({\mathbf{R}},{\mathbf{R} } ^{^{\prime}},\omega) – k_{0}^{2}\int \limits _{{V_{p}}}{d{\mathbf{R}}^{^{\prime \prime }} G_{ik}^{(0)}({\mathbf{R}},{\mathbf{R}}^{^{\prime\prime}},\omega){\rm X}_ { kl}^{(p)} ({\mathbf{R}}^{^{\prime\prime}},\omega) G_{lj}^{(0)}({\mathbf{R}}^ {^{\prime\prime}}, {\mathbf{R}}^{^{\prime}}, \omega)}, \\\end{aligner}$$
(1)
où l’intégrale est supérieure à la taille de la petite nanoparticule, \(k_{0}^{{}}=\omega/c\)Et le c est la vitesse de la lumière, et les indices inférieurs signifient x, y et z dans le système de coordonnées cartésiennes. Ici et ci-dessous, nous utilisons la somme de la notation d’Einstein, ce qui signifie que \(A_{ij} B_{jl}=\sum \limits_{j=x,y,z}{A_{ij}B_{jl}=A_{ix}B_{xl}+A_{iy}B_{yl ) } + A_{iz} B_{zl}}\). dans l’éq. (1) \(G_{ij}^{(R)}({\mathbf{R}},{\mathbf{R}}^{^{\prime}},\omega)\) est l’effet de nanoparticules plus petites sur la fonction pseudo-verte due à la redistribution locale du champ.
Sous le concept de sensibilité effective, il a été développé en20la susceptibilité effective des grosses nanoparticules noyées dans un pseudo-vide (le « nouveau » milieu constitué d’un environnement et de petites nanoparticules) décrite par la fonction verte \(G_{ij}^{(m)}({\mathbf{R}},{\mathbf{R^{\prime}}},\omega)\) Il peut être calculé selon
$$\Xi_{ij}^{(b)}({\mathbf{R}},\omega) = \left[ {\left( {{\rm X}_{ij}^{(b)} ({\mathbf{R}},\omega )} \right)^{ – 1} – k_{0}^{2} \int\limits_{{V_{v} }} {d{\mathbf{R}}^{^{\prime}} G_{ji}^{(R)} ({\mathbf{R}},{\mathbf{R}}^{^{\prime}} ,\omega )} } \right]^{-1}, $$
(2)
où \({\rm X}_{ij}^{(b)}({\mathbf{R}},\omega)\) C’est la susceptibilité des grosses nanoparticules qui peut être évaluée à partir de l’équation suivante22,23qui ne s’applique qu’aux nanoparticules sphériques à coquilles :
$${\rm X}_{ij}^{(b)}({\mathbf{R}},\omega) = \delta_{ij}{\rm X}^{(b)} (\omega) ,\,{\rm X}^{(b)} (\omega) = 3\ ; \frac{{(\varepsilon_{2}-\varepsilon_{m})(\varepsilon_{1}+2\varepsilon_{2}) + f_{1}(\varepsilon_{1}-\varepsilon_{2})) ( \varepsilon_{m} + 2 \varepsilon_{2})}{(\varepsilon_{2}+2\varepsilon_{m})(\varepsilon_{1}+2\varepsilon_{2}) + f_{1}( 2\varepsilon_{2}-2\varepsilon_{m})(\varepsilon_{1}-\varepsilon_{2})}},$$
(3)
où2 est le rayon extérieur, ε1 et ε2 est le noyau (rayon a1) et les fonctions de gaine isolante, respectivement. La fraction volumique de base est \(f_{1} = {{a_{1}^{3}}\mathord {\left/{\vphantom {{a_{1}^{3}}{a_{2}^{3}}}} \right.\kern-\nulldelimiterspace}{a_{2}^{3}}}.\) Il est à noter que l’idée de vulnérabilité effective est articulée depuis longtemps (voir par exemple23, classe. 2) À la suite de l’utilisation de cette idée, nous pouvons nous référer à l’obtention de la formule de Lorenz-Lorentz pour la polarisation de la sphère dans un champ extérieur homogène. également \({\rm X}_{ij}^{(b)}({\mathbf{R}},\omega)\) Les processus auto-agissants des particules dans le milieu reflètent les propriétés homogènes. Mais, \(\Xi_{ij}^{(b)}({\mathbf{R}},\omega)\) Il prend en compte les processus d’auto-réaction à travers les petites nanoparticules, et dépend bien sûr de la distance entre les nanoparticules (voir Figure 1).
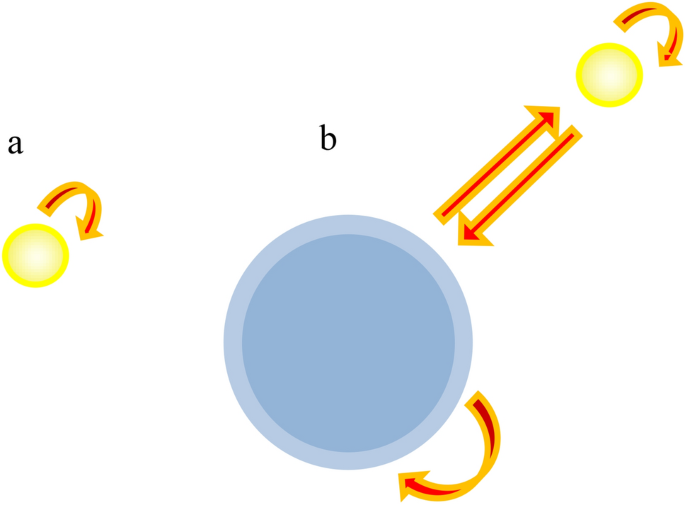
Schéma des processus d’auto-emploi pris en compte lorsque les sensibilités effectives \({\rm X}_{ij}^{(b)}({\mathbf{R}},\omega)\) Et le \({\rm X}_{ij}^{(p)}({\mathbf{R}},\omega)\)– (une); Et le \(\Xi_{ij}^{(b)}({\mathbf{R}},\omega)\)– (B).
Il convient de noter que nous avons mis en place une procédure d’auto-cohérence lors du calcul des forces motrices cérébrales entre les nanoshells. L’autocohérence a été réalisée dans le cadre de la méthode développée dans20. Une procédure auto-cohérente similaire a été montrée dans24. Mais dans le présent travail, nous avons effectué l’auto-cohérence avec la méthode de la fonction pseudo-verte du vide et obtenu des équations auto-cohérentes pour la sensibilité effective des nanoparticules compte tenu du fait que les nanoparticules ne sont pas ponctuelles et ont une forme et des dimensions, contrairement à dans24 La même auto-cohérence des moments dipolaires des nanoparticules a été réalisée dans une approximation de type point dipolaire. Ainsi, l’intérêt du présent travail n’est pas seulement l’auto-cohérence mais aussi la prise en compte de l’hétérogénéité des champs locaux au sein et au niveau des nanoparticules.
À cet égard, il convient de noter que les forces motrices cérébrales ont été calculées aux points de gradients extrêmes des champs locaux, et bien sûr, les intégrales de la densité des forces motrices cérébrales étaient supérieures à la taille de la coque des nanoparticules dans le champs hotspot du champ local.
Pour calculer l’intensité du champ local (y compris les « points chauds »), l’équation d’auto-cohérence (l’équation dite de Liebmann-Schwinger)25 doit être utilisé
$$ \ start {align} E_{i} ({\mathbf{R}},\omega) & = E_{i}^{(0)}({\mathbf{R}},\omega)\\& \, \, \, \, – k_{o}^{2}\int \limits _{{V_{v}}}{d{\mathbf{R}}^{^{\prime}} G_{ij } ^{(m)} ({\mathbf{R}},{\mathbf{R}}^{^{\prime}},\omega)\Xi_{jl}^{(v)} ({\mathbf {R}}^{^{\prime}},\omega) E_{l}^{(0)} ({\mathbf{R}}^{^{\prime}},\omega)}. \\ \ fin {aligner} $$
(4)
Ensuite, la densité de force (force par unité de volume) agissant sur la grande nanoparticule peut être écrite comme
$$ F_{i} ({\mathbf{R}}) = \left({P_{j}({\mathbf{R}})\cdot \frac {\partial }{{\partial x_{j}} }} \right) E_{i} ({\mathbf {R}}), $$
(5)
où \(P_{j} ({\mathbf{R}}) = \varepsilon_{0}\Xi_{jl}^{(v)} ({\mathbf{R}}) E_{l}^{0}( {\mathbf {R}})\) est la polarisation (moment dipolaire local) de l’enveloppe des nanoparticules.
Étant donné que la polarisation et le champ dans la formule (5) sont des propriétés locales et que la polarisation est distribuée en continu sur la coque d’une grosse particule, la force agissant sur un élément du volume de la coque est calculée comme l’intégrale (5) sur ce volume. En ce sens, on parle de « densité » de force. Cela signifie que nous calculons la force agissant sur la petite taille de la nanoparticule pour différentes régions de ces nanoparticules. Et puisque la force (5) est déterminée par le gradient de champ local, lors du calcul des composantes normale et tangentielle de la force agissant sur un élément du volume de la coque, nous choisissons cet élément qui correspond à la valeur maximale du gradient de champ (hotspot Région).
Par exemple, l’éq. (5) est égal à l’équation de densité de force dans l’équation. (3.62) de26. Si la densité du moment dipolaire, c’est-à-dire la polarisation, est remplacée par le moment dipolaire, alors l’équation. (5) est la puissance égale au premier terme de l’équation. (2.2) de27. Alors en utilisant (4) on obtient
$$ \ start {collect} F_{i} ({\mathbf{R}}) = \left({\varepsilon_{0}\Xi_{jk}^{(v)}({\mathbf{R}}) E_{k}^{0}({\mathbf{R}})\cdot \frac {\partial } {{\partial x_{j}}} \right) \cdot \hfill \\\left[ {E_{i}^{(0)} ({\mathbf{R}},\omega ) – k_{o}^{2} \int\limits_{{V_{v} }} {d{\mathbf{R}}^{^{\prime}} G_{is}^{(m)} ({\mathbf{R}},{\mathbf{R}}^{^{\prime}} ,\omega )\Xi_{sl}^{(v)} ({\mathbf{R}}^{^{\prime}} ,\omega )E_{l}^{(0)} ({\mathbf{R}}^{^{\prime}} ,\omega )} } \right]. \ hfill \\ \ end {pluriel} $$
Considérant qu’aux distances autour de la dimension linéaire caractéristique des nanoparticules, le champ externe est plus ou moins constant, cette équation peut se réduire à l’équation suivante
$$ \ start {collect} F_{i} ({\mathbf{R}}) = – k_{o}^{2}\varepsilon_{0}\Xi_{jk}^{(v)}({\mathbf {R}}) E_{k}^{0}({\mathbf{R}})\cdot\hfill \\\int \limits _{{V_{v}}}{d{\mathbf{R}} ^{^{\prime}}\frac{\partial }{{\partial x_{j}}} G_{est}^{(m)}({\mathbf{R}},{\mathbf{R}} ^{^{\prime}},\omega)\Xi_{sl}^{(v)}({\mathbf{R}}^{^{\prime}},\omega) E_{l}^{( 0 )} ({\mathbf{R}}^{^{\prime}},\omega).}\hfill \\\end{collect}$$
(6)
Notez que dans (6) le différentiel est sur les composants \ ({\mathbf {R}} \). Il est clair que l’effet de la force sur l’unité de surface de la croûte peut modifier les propriétés de la croûte jusqu’à sa destruction.
Dans le modèle de susceptibilité elliptique, le tenseur de champ homogène \(\Xi_{jk}^{(v)} ({\mathbf{R}})\) Ne dépendez pas du format23,24En d’autres termes \(\Xi_{jk}^{(v)}({\mathbf{R}})\à \Xi_{jk}^{(v)}\). Ensuite, l’origine de la dépendance de la force de (6) aux coordonnées est due à la distribution locale du champ à la surface de la grosse nanoparticule uniquement – par dépendance de la fonction verte \(G_{est}^{(m)}({\mathbf{R}},{\mathbf{R^{\prime}}},\omega)\) sur moi s [see (6)]. N’oubliez pas que le champ extérieur \(E_{l}^{(0)} ({\mathbf{R}},\omega)\) Elle est constante dans l’approximation en champ proche. Ensuite, il peut être obtenu à partir de (6)
$$ F_{i} ({\mathbf{R}}) = – k_{o}^{2}\left( {\varepsilon_{0}\Xi_{jk}^{(v)}\cdot\int\ limites _{{V_{v}}{d{\mathbf{R}}^{^{\prime}}\frac {\partial }{{\partial x_{j}}} G_{is}^{( m )} ({\mathbf{R}},{\mathbf{R}}^{^{\prime}},\omega)\Xi_{sl}^{(v)}}} \right) E_{k } ^{(0)}E_{l}^{(0)}. $$
(sept)
Étant donné que les emplacements des « points chauds » (domaines de domaine local fort) sont déterminés par la dépendance de la fonction verte vis-à-vis de sles forces agissant sur les grosses nanoparticules (éjectées) seront concentrées dans les points chauds (Fig. 3c).





