A l’infini, les droites et les carrés ont le même nombre de points

Dans des publications précédentes, nous avons prouvé que deux groupes sont de même taille s’il existe une correspondance biunivoque entre les items des deux groupes. L’application de ce principe au théorème de l’infini de Cantor conduit à la conclusion étrange mais valable que le nombre de points sur un segment de droite est le même que le nombre de points sur un carré. Pour montrer que cela est vrai, voici une image d’un segment de longitude unitaire et d’un carré unitaire.

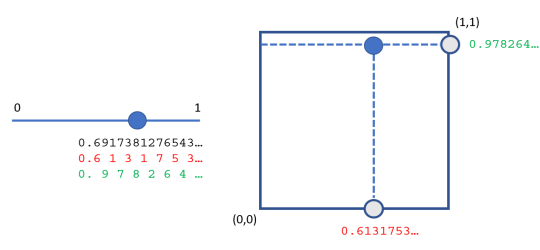
Choisissons un point sur le segment de droite. Supposons 0,6917381276543…. Il est matérialisé par un gros point bleu sur le segment droit de gauche. Si ce point correspond à nombre irrationnel, Cela continue indéfiniment sans se répéter ni montrer un schéma reconnaissable.

Nous diviserons ce nombre en deux nombres. Le premier nombre est tous les autres nombres. Ce nombre est affiché en rouge sous le segment de ligne, qui est précisément 0,6131753…. Les nombres restants constituent le deuxième nombre, affiché en vert. C’est 0,978264….

Ainsi, un nombre entre zéro et un peut être divisé en deux nombres entre zéro et un. Nous pouvons prendre ces deux nombres comme coordonnées x et y sur le carré unitaire illustré à droite. Ils marquent le point bleu indiqué dans la case à droite. Ainsi, le point bleu sur le segment de droite se rapproche du point bleu sur le carré.

Pour chaque point du segment de droite, il n’y a qu’un seul point bleu dans le carré. La taille des groupes infinis sur un segment droit et sur un carré est exactement la même. L’extension de cet argument montre que le nombre de points dans un cube est le même que le nombre de points sur un segment de droite. C’est étrange et inattendu.

Il est également possible d’inverser la cartographie de la section carrée à la section droite. Prenez les deux coordonnées qui définissent le point bleu dans le carré et mélangez-les pour obtenir un seul nombre. Deux nombres entre zéro et un peuvent toujours être combinés pour obtenir un nombre entre un et zéro. Ce nouveau nombre est le point sur le segment de droite.

Puisqu’il existe une correspondance un à un de chaque point sur le segment droit pour chaque point du carré, le nombre de points sur un segment droit est le même que le nombre de points dans le carré.

Mais ne pouvez-vous pas dessiner une ligne droite et un carré sur une feuille de papier et faire la cartographie ? N’est-ce pas un exemple d’infini dans la réalité ? Non, chaque point est censé être mesuré avec une précision illimitée. En réalité, la précision est toujours limitée. Ainsi, la conclusion qu’il n’y a pas de fin en fait est solide.

Ce résultat contre-intuitif, conduit par la théorie de Cantor de l’étrange infini. Cependant, c’est une propriété valide infinie.

le prochain: Nous montrerons que toute la Bibliothèque du Congrès est numériquement codée sur presque tous les numéros choisis au hasard.

Voici la partie 1 : Pourquoi l’infini n’existe pas réellement. Quelques exemples montreront les résultats absurdes qui découlent de l’hypothèse qu’il y a de l’infini dans le monde qui nous entoure comme en mathématiques. Dans une série de cinq articles, j’explique la différence entre ce que l’infini signifie – et ne signifie pas – en tant que concept.

Et le

Partie 2. Infinity explique que l’univers a un début. Les conséquences logiques d’un passé littéralement infini sont absurdes, comme le montrera une simple illustration. L’absurdité qu’un passé infini pourrait créer, bien qu’il ne s’agisse pas d’une preuve mathématique définitive, est une preuve solide que notre univers a eu un commencement.

Vous aimerez aussi lire : Oui tu peux manipulation à l’infini En mathématiques. Les superpériodes sont plus grandes (et plus petites) que le nombre moyen – et même meilleures ! (Jonathan Bartlett)